최근들어 신나게 그래프 관련 알고리즘 문제들을 실버 단계부터 풀고 있다.
그러던중 플로이드-워셜 알고리즘으로 풀어야 하는 문제를 발견하여 해당 개념을 공부하고 구현해봤다.
해당 알고리즘으로 풀어야 하는 문제는 백준 - 케빈 베이컨의 6단계 법칙 1389 이다.
// 입력
5 5 // 유저 수(N), 친구 관계 수 (M)
1 3
1 4
4 5
4 3
3 2
// 출력
3N 개의 노드와 M 개의 간선들로 이뤄진 그래프 V가 있을 때 자신을 제외한 다른 노드들간의 경로의 합이 가장 작은 노드를 찾는 문제이다.
플로이드 워셜 알고리즘
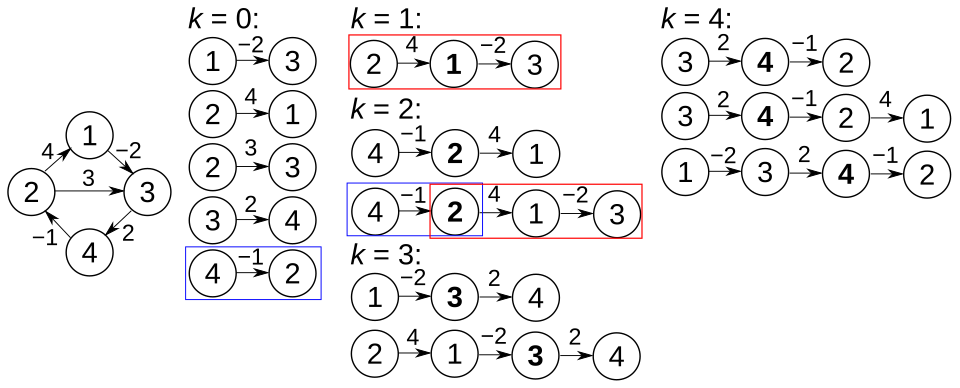
해당 알고리즘은 어떤 그래프 G 에서 i,j 노드를 잇는 최단 경로를 구할 때 그래프 상 다른 노드 집합 K 를 경유하거나 경유하지 않는 경로를 모두 구하고 해당 경로의 최소값을 최단 경로라 정의하는 방식이다.
즉, 1번부터 N번까지의 노드를 가진 그래프에서 가질 수 있는 K 의 집합은 {0,1,2 , ... N} 이다. (0 은 아무런 노드를 경유하지 않는 경우이다.)
이 때 최단 경로 (Shortest Path) 를 의미하는 sp(i,j,k) 는 다음과 같은 점화식으로 표현 할 수 있다.
점화식을 표현하는 인수들은 다음과 같다.
- i : 출발 노드
- j : 도착 노드
- k : 가질 수 있는 경유지 노드들중 최대 노드 (예를 들어 k가 2라면 집합은 {0,1,2} 이다.)
sp(i,j,k) = min(sp(i,j,k-1), sp(i,k,k-1) + sp(k,j,k-1))
이 때 k 가 0이라면 sp(i,j,0) = w[i][j] 이다. (w는 i와 j를 잇는 경로를 담은 2차원 배열)
점화식이 이렇게 표현되는 것은 매우 자명하다.
i,j 를 잇는 최소 경로는 k 노드를 거치지 않는 경로인 sp(i,j,k-1) 와 k 노드를 거치는 경로인 sp(i,k,k-1) + sp(k,j,k-1) 경로 중 하나이기 때문이다.
재귀 (탑다운) 방식으로 풀어보기
해당 점화식을 이용하여 탑다운 방식으로 풀어보자
const fs = require("fs");
const path = require("path");
const filePath =
process.platform === "linux"
? "/dev/stdin"
: path.join(__dirname, "input.txt");
const inputs = fs.readFileSync(filePath).toString().trim().split("\n");
const [N, _] = inputs[0].split(" ").map(Number);
const edges = inputs.slice(1).map((line) => line.split(" ").map(Number));
const W = Array.from({ length: N + 1 }, () => Array(N + 1).fill(Infinity));
edges.forEach(([a, b]) => {
W[a][b] = 1;
W[b][a] = 1;
});
// 자기 자신으로 가는 경로는 0
for (let i = 1; i <= N; i++) {
W[i][i] = 0;
}
const shortestPath = (i, j, k) => {
if (k === 0) {
return W[i][j];
}
return Math.min(
// k 경로를 거치지 않는 최단 경로
shortestPath(i, j, k - 1),
// k 경로를 거치는 최단 경로
shortestPath(i, k, k - 1) + shortestPath(k, j, k - 1)
);
};
let result = 0;
let min = Infinity;
// 모든 노드들에 대해서 최단 경로를 가지는 노드 구하기
for (let start = 1; start <= N; start++) {
let totalDepth = 0;
for (let end = 1; end <= N; end++) {
if (start === end) continue;
totalDepth += shortestPath(start, end, N);
}
if (totalDepth < min) {
min = totalDepth;
result = start;
}
}
console.log(result);이렇게 풀면 데이터 개수가 아주 작은 경우에는 무리가 없지만 데이터 개수가 늘어나니 시간 초과가 뜨며 통과가 되지 않는다.
그도 그럴 것이 메모이제이션이 동반되지 않은 재귀호출 메소드의 시간 복잡도는 지수적으로 증가하기 때문이다.
T[K] 를 sp(i,j,k) 의 시간 복잡도라고 정의한다면 T[K] = 3 * T[K-1] 이라 할 수 있다. (sp(i,j,k) 는 k-1 개의 경유지를 순회하는 함수를 3번 호출한다.)
이 때 T[0] = 1 일 때 T[1] = 3, T[2] = 3 ** 2 , ... T[K] = 3 ** K 가 된다.
동적 프로그래밍으로 풀어보기
이번엔 탑다운이 아닌 바텀업 방식으로 풀어보자
경유하는 노드가 없는 경우부터해서 모든 노드를 경유하는 동안 W[i][j] 값들을 업데이트 해나가며 풀이 할 수 있으며 이 과정을 통해 이전에 구해둔 최적 경로들을 재사용하여 불필요한 연산을 줄일 수 있다.
const fs = require("fs");
const path = require("path");
const filePath =
process.platform === "linux"
? "/dev/stdin"
: path.join(__dirname, "input.txt");
const inputs = fs.readFileSync(filePath).toString().trim().split("\n");
const [N, _] = inputs[0].split(" ").map(Number);
const edges = inputs.slice(1).map((line) => line.split(" ").map(Number));
const W = Array.from({ length: N + 1 }, () => Array(N + 1).fill(Infinity));
edges.forEach(([a, b]) => {
W[a][b] = 1;
W[b][a] = 1;
});
// 자기 자신으로 가는 경로는 0
for (let i = 1; i <= N; i++) {
W[i][i] = 0;
}
const shortestPath = (N, W) => {
// 경유할 정점 K
for (let K = 0; K <= N; K++) {
for (let i = 1; i <= N; i++) {
for (let j = 1; j <= N; j++) {
W[i][j] = Math.min(
// K 노드를 경유 하지 않는 경우
W[i][j],
// K 노드를 경유 하는 경우
W[i][K] + W[K][j]
);
}
}
}
return (
W.slice(1)
.map((row) => row.slice(1).reduce((acc, cur) => acc + cur))
.findIndex((total, _, array) => total === Math.min(...array)) + 1
);
};
console.log(shortestPath(N, W));이 과정을 통해 가능한 W[i][j] 값들을 최단 경로들로 업데이트해나감으로서 정답을 쉽게 구할 수 있다.