abonglog최근 그래프 알고리즘을 공부하며 순열 그래프에서 순열 사이클의 개수를 구하는 문제를 풀어봤다. 백준 - 10451 순열 사이클
다만 이 과정에서 나는 순열 그래프의 정의에 대해서 이해하지 못했어서 결국 이상한 스파게티같은 코드를 작성했고, 결국 풀이를 보고야 말았다.
다만 풀이들을 보다보니 경우의수와 그래프 자료구조가 관련이 있더라
그래서 경우의 수를 계산하는 것과 그래프 자료구조의 관련성을 정리해본다.
순열이란
순열이란 N 개의 원소를 가진 집합에서 원소 r 개를 뽑아 특정한 순서로 배열하는 것을 의미한다.
이 때 순서에 따른 중복을 허용하지 않는 직순열과 중복을 허용하는 중복순열로 나뉜다.
직순열 (Permutation)
직순열은 원소 N 개가 담긴 집합에서 중복을 허용하지 않고 원소 r 개를 뽑아 존재하는 경우의 수를 생성하는 것과 같다.
중복을 허용하지 않는다는 것은 한 번 뽑은 원소를 다시 포함하지 않는 다는 것을 의미한다.
N 개의 원소에서 r 개를 뽑을 때 까지의 경우의 수는 N * N -1 * ... N - r - 1 개이며 분모 분자에 (n-r)! 를 곱해주면 N!/(n-r)! 이 나온다.
n 개의 원소에서 r 개를 뽑는 permutation 메소드는 그래프의 DFS 로 구현 가능한데 이유는 다음과 같다.
[1,2,3] 으로 이뤄진 집합에서 3개를 뽑을 때 나타나는 경우의 수들을 생각해보자
- 첫 번째 숫자가 1 인 경우 가능한 경우의 수는 [1,2,3], [1,3,2]
- 첫 번째 숫자가 2 인 경우 .... [2,1,3], [2,3,1]
- 세 번째 숫자가 3인 경우 .... [3,1,2] , [3,2,1]
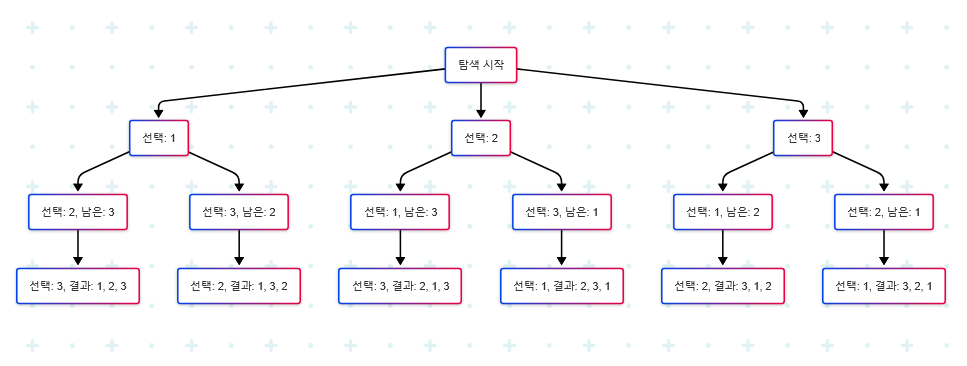순열을 생성하며 만들어진 결정 트리
이렇게 순열을 생성하는 과정은 어떤 결정을 순차적으로 내리는 과정으로 볼 수 있으며 결정 과정을 시각화하면 결정트리 또는 상태 공간 트리 형태가 된다.
각 결정 트리의 레벨 l의 노드의 개수는 N 개의 원소에서 l 개를 뽑는 경우의 수와 같다.
이렇게 순열을 결정 트리 형태로 그려두고 보면 가능한 모든 경우의 수를 구하는 것 은 결정 트리의 정점에서 연결부위가 없는 leaf node 까지의 모든 경로 를 구하는 것과 같음이 직관적으로 이해가 된다.
const permutation = (array, r) => {
if (r > array.length) {
return [];
}
if (r === 1) {
return array.map((value) => [value]);
}
const result = [];
for (let index = 0; index < array.length; index++) {
// 시점 선택
const current = array[index];
// 가능한 다음 자식 노드들 선택, 중복을 허용하지 않기에 자기자신 제거
const remaining = [...array.slice(0, index), ...array.slice(index + 1)];
// 재귀적으로 가능한 모든 경로 탐색 (DFS)
const permutations = permutation(remaining, r - 1);
// 시점과 자식 노드 경로를 합쳐서 결과에 추가
for (const permutation of permutations) {
result.push([current, ...permutation]);
}
}
return result;
};
console.log(permutation([1, 2, 3], 3));[
[ 1, 2, 3 ],
[ 1, 3, 2 ],
[ 2, 1, 3 ],
[ 2, 3, 1 ],
[ 3, 1, 2 ],
[ 3, 2, 1 ]
]중복 순열 (Permutation with Repetition)
중복 순열은 N 개의 집합에서 r개의 원소를 뽑을 때 이전에 뽑은 경우를 허용하는 순열이다.
예를 들어 [1,2,3] 에서 3개를 뽑는 경우 [1,1,1] 도 가능한 경우로 취급하는 것이다.
const permutationWithRepetition = (array, r) => {
if (r > array.length) {
return [];
}
if (r === 1) {
return array.map((value) => [value]);
}
const result = [];
for (let index = 0; index < array.length; index++) {
// 시점 선택
const current = array[index];
// 가능한 다음 자식 노드들 선택, 중복을 허용하기 때문에 모든 노드 선택
const permutations = permutationWithRepetition(array, r - 1);
// 시점과 자식 노드 경로를 합쳐서 결과에 추가
for (const permutation of permutations) {
result.push([current, ...permutation]);
}
}
return result;
};
console.log(permutationWithRepetition([1, 2, 3], 3));[
[ 1, 1, 1 ], [ 1, 1, 2 ], [ 1, 1, 3 ],
[ 1, 2, 1 ], [ 1, 2, 2 ], [ 1, 2, 3 ],
[ 1, 3, 1 ], [ 1, 3, 2 ], [ 1, 3, 3 ],
[ 2, 1, 1 ], [ 2, 1, 2 ], [ 2, 1, 3 ],
[ 2, 2, 1 ], [ 2, 2, 2 ], [ 2, 2, 3 ],
[ 2, 3, 1 ], [ 2, 3, 2 ], [ 2, 3, 3 ],
[ 3, 1, 1 ], [ 3, 1, 2 ], [ 3, 1, 3 ],
[ 3, 2, 1 ], [ 3, 2, 2 ], [ 3, 2, 3 ],
[ 3, 3, 1 ], [ 3, 3, 2 ], [ 3, 3, 3 ]
]이전 직순열과 다른점은 가능한 자식 노드에 자식 노드도 포함한 것이다.
중복 순열에 가능한 경우의 수는 N ** r 개이다.
생각해보면 각 레벨에 가능한 모든 노드의 개수가 N ** r 개이기 때문이다.
조합 (Combination) (중복을 허용하지 않는)
중복을 허용하지 않는 조합은 N 개의 집합에서 원소 r개를 뽑아 부분집합을 생성 할 때 내부 원소의 순서와 상관 없이 내부 원소들이 모두 같다면 집합을 같은 집합으로 고려하는 것이다.
예를 들어 순서쌍 {1,2,3} 과 {3,2,1} 은 같은 조합으로 보는 것이다.
이 경우 결정 트리를 생성 할 때 중복을 허용하지 않기 위해 몇 가지 규칙을 이용 할 수 있는데 이 경우에는 부모 노드는 매번 자식노드보다 값이 커야 한단 규칙을 적용 할 수 있다.
부모노드가 자식노드보다 큰 값을 갖는다면 i 번째 노드를 기준으로 했을 때 i-1 번째 이하 노드에서 선택된 노드들을 이용한 조합을 만들지 않을 수 있기 때문이다.
const combination = (array, r) => {
const sortedArray = array.sort((a, b) => a - b); // 중복을 허용하지 않기 위해 값을 정렬
if (r > sortedArray.length) {
return [];
}
if (r === 1) {
return sortedArray.map((value) => [value]);
}
const result = [];
for (let index = 0; index < sortedArray.length; index++) {
const current = sortedArray[index];
// 자신보다 큰 값들만을 이용하여 결정 트리 생성
const remaining = sortedArray.slice(index + 1);
const combinations = combination(remaining, r - 1);
for (const combination of combinations) {
result.push([current, ...combination]);
}
}
return result;
};
console.log(combination([1, 2, 3, 4], 3));[
[ 1, 2, 3 ], [ 1, 2, 4 ],
[ 1, 3, 4 ], [ 2, 3, 4 ]
]중복 조합 (중복을 허용하는)
이번엔 중복 순열 때 처럼 중복을 허용하는 중복 조합을 생각해보자
기존 조합은 집합의 순서가 다르더라도 내부 원소들이 같다면 같은 집합으로 고려하였기 때문에
결정트리의 부모노드들은 매번 자식노드보다 값이 작아야만 했다. 부모노드보다 값이 작은 조합은 이미 이전 부모 노드에서 다뤄졌기때문이다.
하지만 중복을 허용하는 경우에는 그럴 필요가 없다.
내부 원소들이 같더라도 순서가 다르면 서로 다른 조합으로 취급하기 때문이다.
const combinationWithRepetition = (array, r) => {
if (r > array.length) {
return [];
}
if (r === 1) {
return array.map((value) => [value]);
}
const result = [];
for (let index = 0; index < array.length; index++) {
const current = array[index];
// 자신과 같은 값들만을 이용하여 조합 생성
const combinations = combinationWithRepetition(array, r - 1);
for (const combination of combinations) {
result.push([current, ...combination]);
}
}
return result;
};
console.log(combinationWithRepetition([1, 2, 3], 2)); // [[1, 2], [1, 3], [2, 1], [2, 3], [3, 1], [3, 2]][
[ 1, 1 ], [ 1, 2 ],
[ 1, 3 ], [ 2, 1 ],
[ 2, 2 ], [ 2, 3 ],
[ 3, 1 ], [ 3, 2 ],
[ 3, 3 ]
]회고
어쩌다 보니 풀려고 했던 문제인 순서쌍 사이클과는 관련 없는 내용을 정리했다.
그래도 뭐 가물가물했던 확통 지식을 다시 되짚어봐서 좋았다.
좀 더 흥미로웠던건 단순 공식으로 외웠던 경우의 수들을 결정 트리에서 가질 수 있는 노드의 개수로 바라보는게 좀 더 익숙해졌단 것이다. 크캭